Measurements on the LRK350-20-13 in flight
on 23.9.2001

Because we have the very nice and light  DataLogger , which has a "direct wire" to the SPEEDY-BL, it was simple to make several climbing flights with the ASW24 . The "direct wire" consists of 5 signal wires which supply the data straight from the SPEEDY-BL from the lower connecting plug. The rpm is measured as the 3-phase field revolving frequency, which is 7 times the propellor rpm, and therefore 7 times as accurate.

We measured with an accuracy of 14 bit:

• motor voltage
• motor current
• propellor rpm
• absolute altitude

The DataLogger will allow airspeed measurement, but since we only want to make energy comparisons (propulsion efficiency) I did not mount the speed sensor that I normally use for measuring polar graphs..

The ASW24 has a wingspan of 3,14m and weighs 3,3kg. 10 Cell packs were used as energy source. Placing the motor LRK350-20-13 and the ESC was not a problem in the spacious fuselage. The propellor was an Aeronaut 15x8. You can see the Picolario in the picture. That is where we fixed the Datalogger.

We started at 16:00 in fairly windy weather in a large meadow. After the first climb you can see a bit of thermal activity (90-120s). At the second descent around 540s, Jochen pitched it down firmly over the whole 70m.

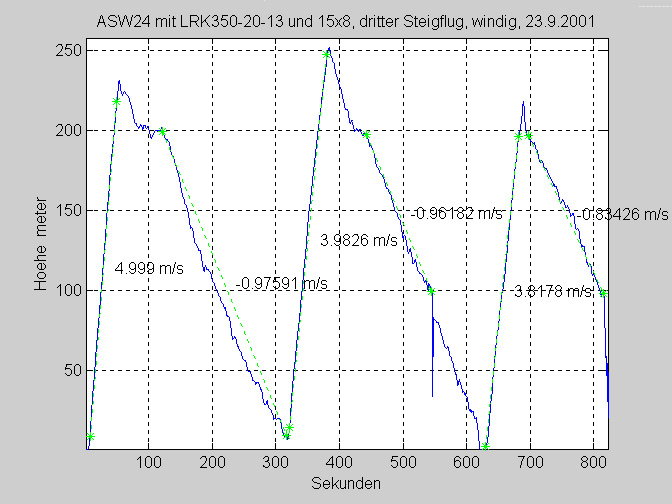
An important result is the sinking speed of approx. -0,95m/s. I will use this figure later to assess the climbing performance. Interesting are the battery voltage and the motor current.

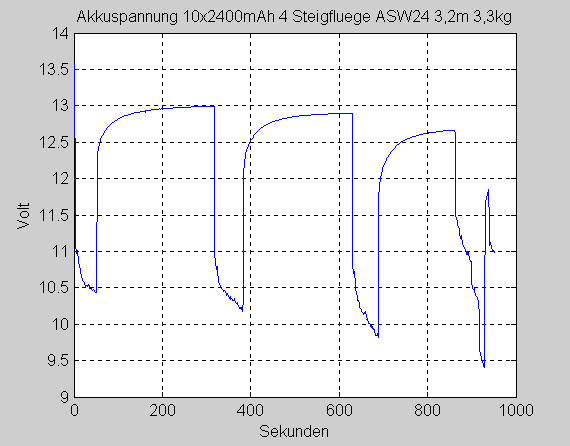
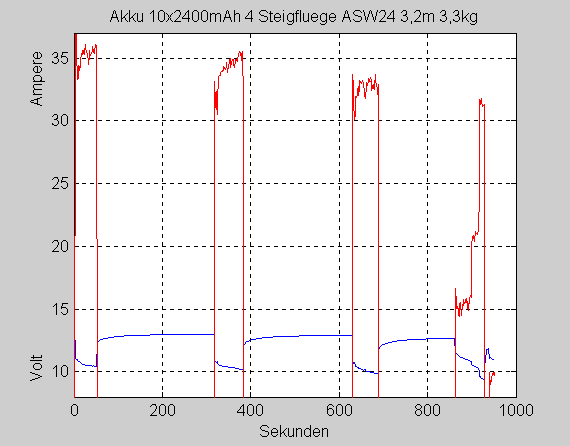
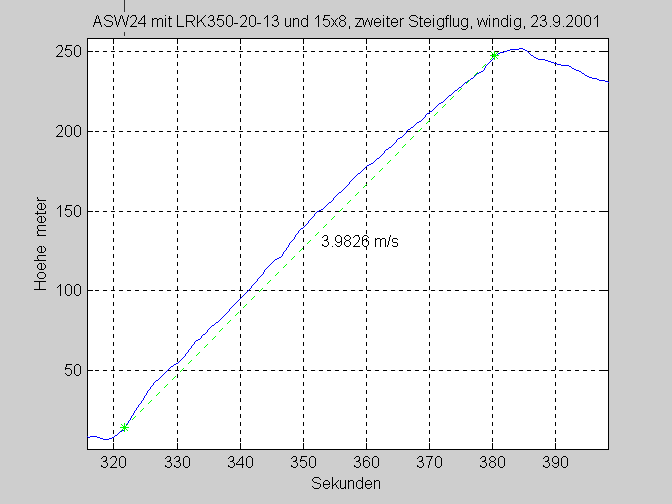
Since the first climb was at 5m/s we will look closer at this climb to see if there are any unusual stretches.

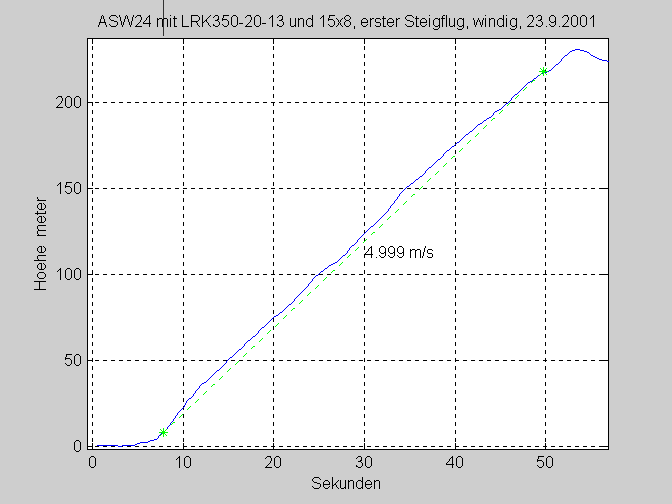
Thanks to the pilot the climb was very steady, no energy from the cells was waisted with stalls. The second climb shows an average rate of climb of 4 m/s.

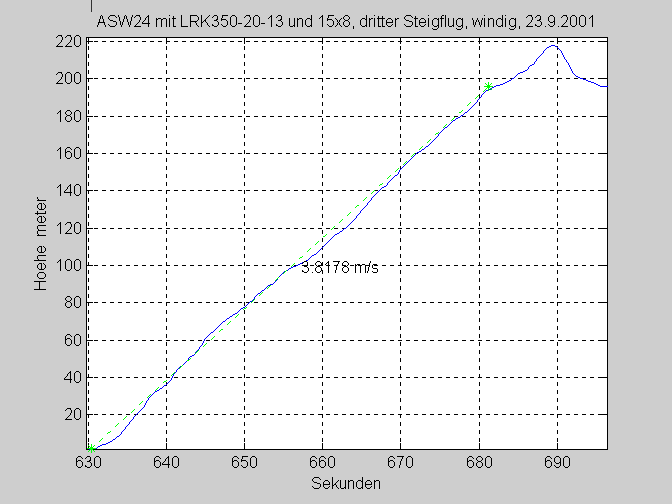
The third climb:

At the fourth climb we have investigated the partial loading at 15A and 22A, on my special request (see current diagram). Full throttle climb needs 35A. I will not discuss partial load here. We concentrate on the average climb #2.

Let's take the section from 320s to 380s, 1 Minute long.

Altitude increase is:

H=h(380)-h(320)=243,5-7,5=236m

The 3,3kg heavy model has aquired a potential energy of:

Ep=m*g*H=3,3*9,81*236=7.640 Joule oder Watt-Sekunden

In the same timespan the model "descended" wit a sink rate of -0,95m/s and has spent potential energy:

Es=m*g*T*v_sink=3,3*9,81*60*0,95=1.845 Joule

The propulsion has transmitted in 60 seconds an amount of energy of:

E=Ep+Es=7.640+1.845=9.485 Joule

to the airframe. The question is, how much energy has the propulsion drawn from the battery?

For that, we only need to calculate the integral of U*I over the 60s between 320s and 280s.

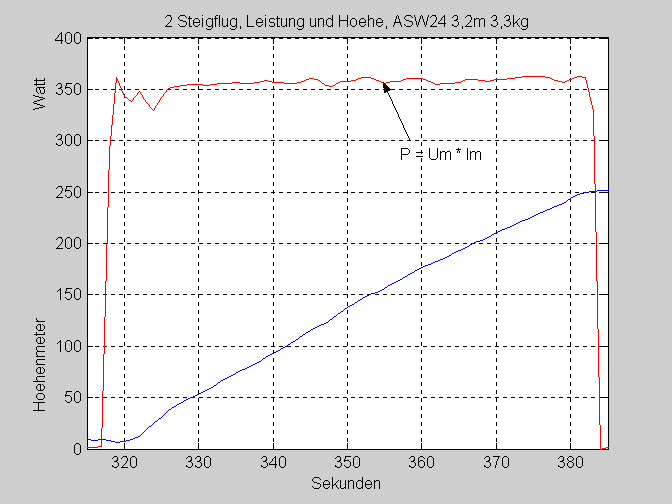
From the battery we used:

E_bat=Sum(U*I)=21.361 Joule (Volt*Amp*Sekunden)

Now we can calculate the overall efficiency: from battery, past the ESC, motor,propellor to the model and the height it gained:

Eta=E/E_bat=9.485/21.361=0,444=44%

I have not seen such a high effiency before, although I build performance models and I have measured several propulsions. This high number results from several favourable aspects:

I will not bore you with the other flights and the 2nd and 3rd battery. Altogether 12 climbs.The efficiency of the first flight was even marginally higher. Overall you can say that the propulsion is very efficient.

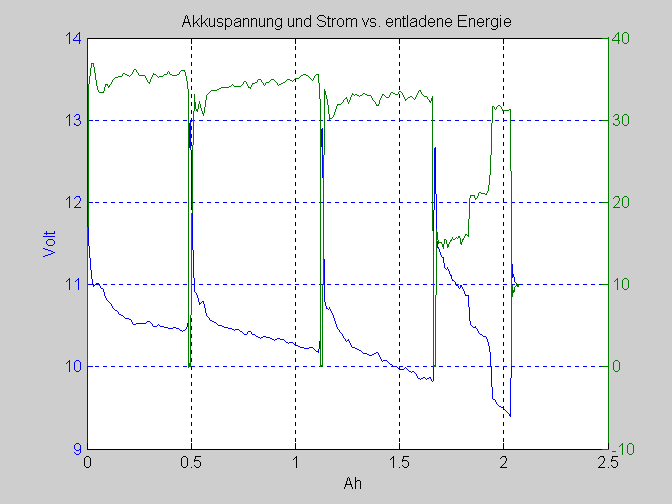
To conclude a graph of the battery voltage, not against time but against the extracted energy (mAh). The green line shows the concurrent motor current. The fourth flight was partial load!