How many windings does my motor need?

This is not easy task to calculate windings count, specially at high motor current. I was looking for an easy mathematical model for some time.

Good News:

I have found such mathematic model and it works until today for all motors that have been build so far. This model works for different windings, different currents and different propellers.

With this model you can know motor revolution for any combination of battery and propeller size. This calculation is accurate down to 3%.

This page states about 20mm stator height with 35mm diameter, there is another page that talks about any stator height.

Basics, known from school, however for commutator motor:

There is Um voltage across the motor. Through the motor flows current Im. The propeller rotates with n

Um - motor voltage
Im - motor current
n - propeller number of revolution

Every motor can be specified by few basic parameters. The simplest are:

Io - idle current (in most cases linear increasing with voltage)

Ri - inner resistance, increasing with temperature

ns(n,Im, ...) - specific number of revolution per volt, dependent of n, Im

 

Two innovations:

1) The specific revolution number per volt ns(Im) will be calculated only from remaining voltage after subtracting voltage drop across inner resistance Ri.

U = Um - Im * Ri

ns(Im) = n / (Um - Im * Ri) = n / U

Measurement example:

Um Im U I n ns no
kns
5.63 8.89 5.31 7.19 3154 594
6.53 11.15 6.12 9.45 3566 582
7.61 13.99 7.11 12.29 4054 571
8.85 17.55 8.22 15.85 4560 555 627
10.21 21.34 9.44 19.64 5083 538
11.59 25.69 10.67 23.99 5563 522 -4.09

We see in the table ns goes down when current goes up. This function is linear and represents some kind of magnetic stiffness. For this linear function we can find no (this is ns at Im=0) and kns - slope of the line. This two parameters are representing any given motor:

ns(Im) = no + kns * Im

 

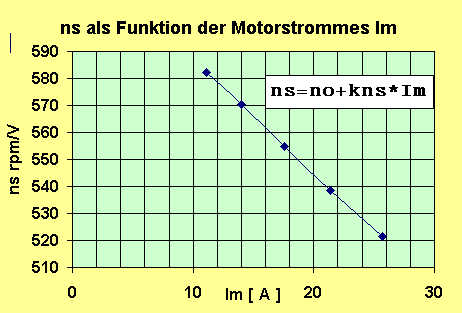
From part of my Measurements can be seen, that no=ns(0) for one motor is absolutely constant, independent of big or small propeller has been rotated by the motor (motor stalled, or rotating without any proper load). The kns is constant also, at my LRK350-20 about -4.1.

But there is even more important regularity:

The product of no=ns(0) and windings number N is constant for any given LRK350 motor independent of windings and wire size.

 

 no * N = W = constant

 

Results:

1. For any stator, rotor combination independent of windings and load the characteristic value W exists. For LRK350-20

W=9420

2. Having requested rpm/volt we can calculated windings count.

3. From windings count and wire size we can calculate inner resistance Ri.

The prove of this method can be found here.

 

Example of simple calculation

Given: (e.g. LRK350-20-11)

Ri=15mOhm, no=820, kns=-4.2 und Io=2A

The inner resistance of the motor controller is: 4mOhm (2+2)

You want run this motor on 8 V with 35 Amp.

Question:

What is the revolution per minute rpm?

 

Solution:

Um = 8V than Uemk = Um - (Ri+Ric) * Im = 7.33V

ns at that current:

ns(35A) = no - kns * Im = 673 rpm/Volt

The rpm is:

n = ns * Uemk = 673 * 7.33 = 4,933 rpm

The mechanical output is (without magnetic losses)

Pmech = Uemk * (Im - Io) = 7.33 V * 33 A= 240 W

For the rpm and power you need an propeller with the 100 watts specific number n100w of:

( n / n100w ) ^ 3 = Pmech / 100

n100w ^3 = n ^3 * 100 / Pmech

n100w = 3685


back to LRK site